The basic inverting amplifier configuration using an op-amp with input impedance Z1 and feedback impedance Zf
If the impedance Z1 and Zf are equal in magnitude and phase, then the closed loop voltage gain is -1,and the input signal will undergo a 1800 phase shift at the output. Hence, such circuit is also called phase inverter. If two such amplifiers are connected in cascade, then the output from the second stage is the same as the input signal without any change of sign
Hence, the outputs from the two stages are equal in magnitude but opposite in phase and such a system is an excellent paraphase amplifier
Referring the above diagram, if the ratio Zf / Z1 = k, a real constant, then the closed loop gain is –k, and the input voltage is multiplied by a factor –k and the scaled output is available at the output. Usually, in such applications, Zf and Z1 are selected as precision resistors for obtaining precise and scaled value of input voltage.
1. PHASE SHIFT CIRCUITS
The phase shift circuits produce phase shifts that depend on the frequency and maintain a constant gain. These circuits are also called constant-delay filters or all-pass filters. That constant delay refers to the fact the time difference between input and output remains constant when frequency is changed over a range of operating frequencies.
This is called all-pass because normally a constant gain is maintained for all the frequencies within the operating range. The two types of circuits, for lagging phase angles and leading phase angles.
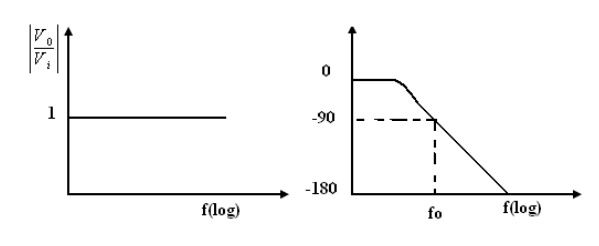
2. Phase-lag circuit:
Phase log circuit is constructed using an op-amp, connected in both inverting and non inverting modes. To analyze the circuit operation, it is assumed that the input voltage v1 drives a simple inverting amplifier with inverting input applied at(-)terminal of op-amp and a non inverting amplifier with a low-pass filter.
It is also assumed that inverting gain is -1 and non-inverting gain after the low-pass circuit
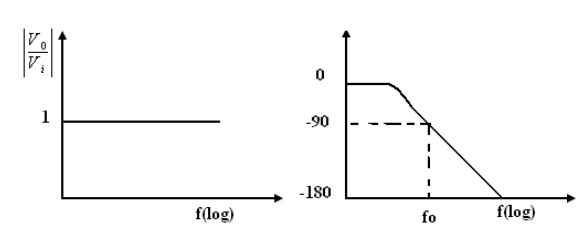
The relationship is complex as defined above equation and it shows that it has both magnitude and phase. Since the numerator and denominator are complex conjugates, their