MESH ANALYSIS:
This is an alternative structured approach to solving the circuit and is based on calculating mesh currents. A similar approach to the node situation is used. A set of equations (based on KVL for each mesh) is formed and the equations are solved for unknown values. As many equations are needed as unknown mesh currents exist.
Step 1: Identify the mesh currents
Step 2: Determine which mesh currents are known
Step 2: Write equation for each mesh using KVL and that includes the mesh currents Step 3: Solve the equations
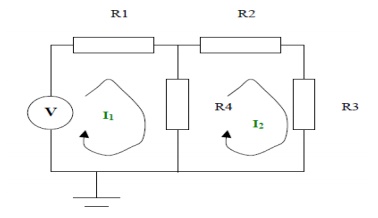
Step 1:
The mesh currents are as shown in the diagram on the next page
Step 2:
Neither of the mesh currents is known
Step 3:
KVL can be applied to the left hand side loop. This states the voltages around the loop sum to zero.
When writing down the voltages across each resistor equations are the mesh currents.
I1R1 + (I1 - I2) R4 - V = 0
KVL can be applied to the right hand side loop. This states the voltages around the loop sum to
zero. When writing down the voltages across ea the equations are the mesh currents.
I2R2 + I2R3 + (I2 - I1) R4 = 0
Step 4:
Solving the equations we get
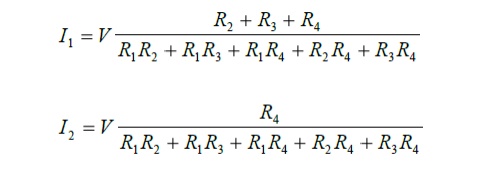
The individual branch currents can be obtained from the these mesh currents and the node voltages can also be calculated using this information. For example:
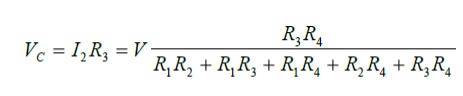
Problem 1:
Use mesh-current analysis to determine the current flowing in (a the 1Ω resistance of the d.c. circuit shown in
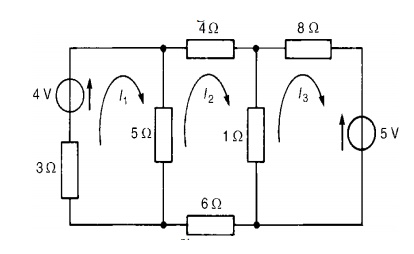
The mesh currents I1, I2 and I3 are shown in Figure
Using Kirchhoff’s voltage law:
For loop 1, (3 + 5) I1 −I2 = 4 …………………………………………………………(1)
For loop 2, (4 + 1 + 6 + 5) I2 −(5) I1 −(1) I3 = 0…………………………………….(2)
For loop 3, (1 + 8) I3 −(1) I2 = 5− ……………………………………………………(3)
Thus
8I1 −5I2 −4 =0
−5I1 + 16I2 −I3 =0
−I2 + 9I3 + 5 =0

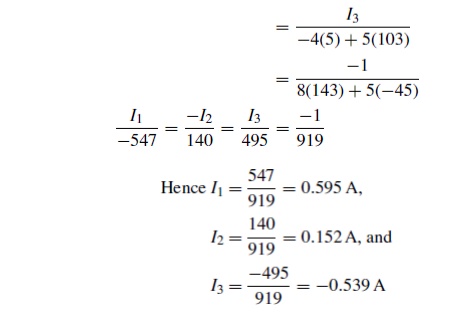
(a) Current in the 5 Ωresistance = I1 −I2
= 0.595 −0.152
= 0.44A
(b) Current in the 1 Ωresistance = I2 −I3
= 0.152 −(−0.539)
= 0.69A
Problem 2: For the a.c. network shown in Figure determine, using mesh-current analysis, (a) the mesh currents I1 and I2 (b) the current flowing in the capacitor, and (c) the active power delivered by the 100∠0◦V voltage source.
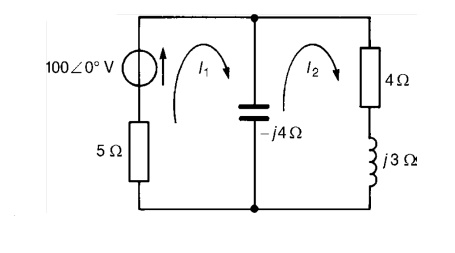
(a) For the first loop
(5−j4) I1 −(−j4I2) =100∠0◦……………………………………………………(1) For the second loop
(4+j3−j4)I2 −(−j4I1) =0 ……………………………………………………… (2)
Rewriting equations (1) and (2) gives:
(5 −j4)I1 + j4I2 −100 =0
j4I1 + (4 −j) I2 + 0 =0 Thus, using determinants,

Thus total power dissipated = 579.97 + 436.81 = 1016.8W = 1020W
Problem 3: Calculate current through -6Ω resistance u
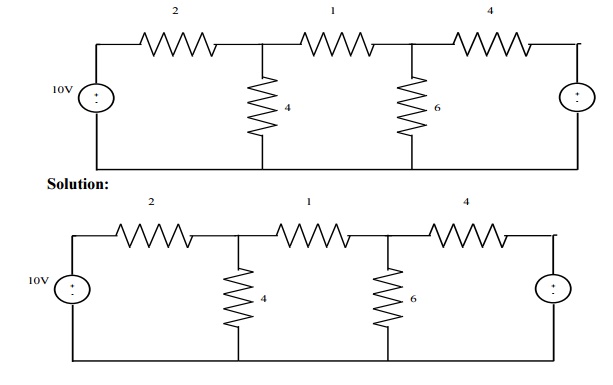
Case(1): Consider loop ABGH ; Apply KVL .
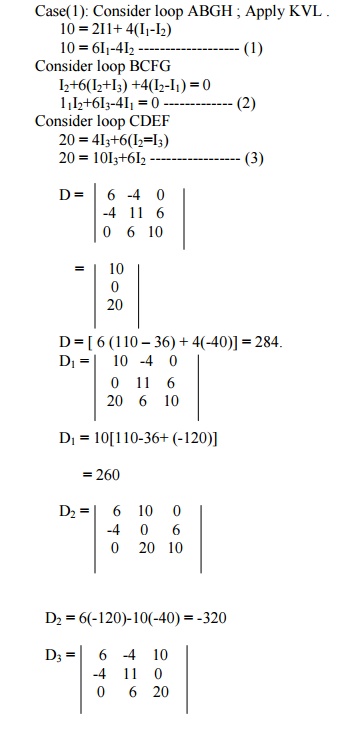
D3 = 6(220) +4(-80) +10(-24)
D3 = 760
I1 = D1/D = 260/284 = 0.915A
I2 = D2/D = -320/284 = -1.1267A I3 = D3/D = 760/284 = 2.676A
Current through 6Ω 2 +Iresistance3 = I
= -1.1267+2.676 = 1.55A
Problem 4: Find the current through branch a-b using mesh analysis.
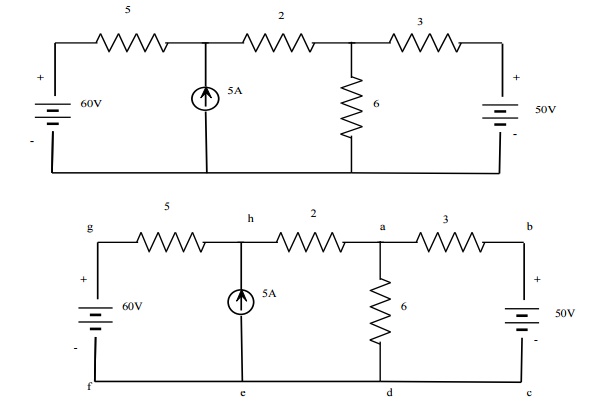
Solution:
Consider loops
Loop HADE - > 5I1+2I2+6(I2-I3) = 60
5I1+8I2-6I3 = 60 ------------ (1)
Loop ABCDA - > 3I3+6(I3-I2) = -50
3I3+6I3-6I2 = -50
9I3-6I2 = -50---------- (2)
I2-I1 = 5A ------------------------- (3)
From (1), (2) & (3).

= -1(-400+360)-(-250) +5(-30)
= 40+250-150
D3 = 140.
I3 = D3/D = 140/-81 = -1.7283
The current through branch ab is 1.7283A which is flowing from b to a.

