KIRCHOFF'S LAW
Kirchoff's First Law - The Current Law, (KCL)
The total current or charge entering a junction or node is exactly equal to the charge leaving the node as it has no other place to go except to leave, as no charge is lost within the node".
In other words the algebraic sum of ALL the currents entering and leaving a node must be equal to zero,
I(exiting) + I(entering) = 0.
This idea by Kirchoff is known as the Conservation of Charge.
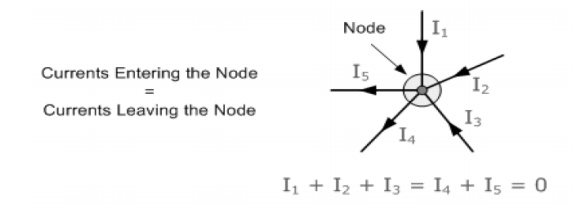
Here, the 3 currents entering the node, I1, I2, I3 are all positive in value and the 2 currents leaving the node, I4 and I5 are negative in value.
Then this means we can also rewrite the equation as; I1 + I2 + I3 - I4 - I5 = 0
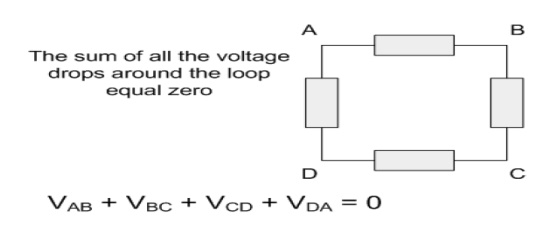
Kirchoff's Second Law - The Voltage Law, (KVL)
"In any closed loop network, the total voltage around the loop is equal to the sum of all the voltage drops within the same loop" which is also equal to zero. In other words the algebraic sum of all voltages within the loop must be equal to zero. This idea by Kirchoff is known as the Conservation of Energy.
Starting at any point in the loop continue in the same direction noting the direction of all the voltage drops, either positive or negative, and returning back to the same starting point. It is important to maintain the same direction either clockwise or anti-clockwise or the final voltage sum will not be equal to zero.
We can use Kirchoff's voltage law when analyzing series circuits.
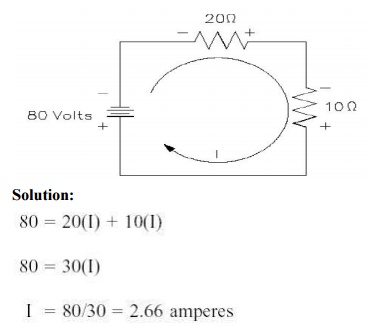
Problem 1:
A current of 0.5 A is flowing through the resistance of 10Ω.Findthepotential difference between its ends.
Solution:
Current I = 0.5A.
Resistance R = 10Ω
Potential difference V =?
V = IR
= 0.5 × 10
= 5V.
Problem: 2
A supply voltage of 220V is applied to a resistor100.FindΩthe current flowing through it.
Solution:
Voltage V = 220V Resistance R = 100Ω Current I = V/ R
= 2 2 0 /100
= 2.2 A.
Problem: 3
Calculate the resistance of the conductor if a current of 2A flows through it when the potential difference across its ends is 6V.
Solution:
Current I = 2A. Potential difference = V = 6. Resistance R = V/I
= 6 /2
= 3 ohm.
Problem: 4
Calculate the current and resistance of a 100 W, 200V electric bulb.
Solution:
Power, P = 100W
Voltage, V = 200V Power p = VI
Current I = P/V
= 100/200
= 0.5A
Resistance R = V /I
= 200/0.5
= 400W.
Problem: 5
Calculate the power rating of the heater coil when used on 220V supply taking 5 Amps.
Solution:
Voltage, V = 220V Current, I = 5A, Power, P = VI
= 220 × 5
= 1100W
= 1.1 KW.
Problem: 6
A circuit is made of 0.4wire,Ωa 150bulbΩand a rheostat120connectedΩ in series. Determine the total resistance of the resistance of the circuit.
Solution:
Resistance of the wire = 0.4ResistanceΩ of bulb = 1 5 0 Ω Resistance of rheostat = 120Ω
In series,
Total resistance, R = 0.4 + 150 +120 = 270.4Ω
Problem : 7
Three resistances of values 2Ω,3Ωconnectedandin series5Ω acrossare20 V,D.C supply
.Calculate (a) equivalent resistance of the circuit (b) the total current of the circuit (c) the voltage drop across each resistor and (d) the power dissipated in each resistor.
Solution:
Total resistance R = R1 + R 2+ R3.
= 2 +3+5 = 10Ω
Voltage = 20V
Total current I = V/R = 20/10 = 2A.
Voltage drop across 2Ωresistor V1 = I R1
= 2× 2 = 4 volts.
Voltage drop across 3Ωresistor V 2 = IR2
= 2 × 3 = 6 volts.
Voltage drop across 5Ωresistor V3 = I R3
= 2 ×5 = 10 volts.
Power dissipated in 2Ωresistor is P1 = I2 R1
= 22 × 2 = 8 watts.
Power dissipated in 3 resistor is P2 = I2 R2.
= 22 × 3 = 12 watts.
Power dissipated in 5 resistor is P3 = I2 R3
= 22 × 5 = 20 watts.
Problem: 8
A lamp can work on a 50 volt mains taking 2 amps. What value of the resistance must be connected in series with it so that it can be operated from 200 volt mains giving the same power.
Solution:
Lamp voltage, V = 50V Current, I = 2 amps.
Resistance of the lamp = V/I = 50/25 = 25 Ω
Resistance connected in series with lamp = r.
Supply voltage = 200 volt.
Circuit current I = 2A
Total resistance Rt= V/I = 200/2 = 100Ω
Rt = R + r 100 = 25 + r
r = 75Ω
Problem: 9
Find the current flowing in the 40Ω Resistor,
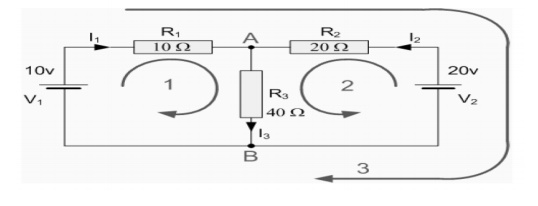
Solution:
The circuit has 3 branches, 2 nodes (A and B) and 2 independent loops.
Using Kirchoff's Current Law, KCL the equations are given as;
At node A: I1 + I2 = I3
At node B: I3 = I1 + I2
Using Kirchoff's Voltage Law, KVL the equations are given as;
Loop 1 is given as: 10 = R1 x I1 + R3 x I3 = 10I1 + 40I3
Loop 2 is given as: 20 = R2 x I2 + R3 x I3 = 20I2 + 40I3
Loop 3 is given as: 10 - 20 = 10I1 - 20I2
As I3 is the sum of I1 + I2 we can rewrite the equations as;
Eq. No 1: 10 = 10I1 + 40(I1 + I2) = 50I1 + 40I2
Eq.No 2: 20 = 20I1 + 40(I1 + I2) = 40I1 + 60I2
We now have two "Simultaneous Equations" that can be reduced to give us the value of both I1 and
I2
Substitution of I1 in terms of I2 gives us the value of I1 as -0.143 Amps
Substitution of I2 in terms of I1 gives us the value of I2 as +0.429 Amps
As: I3 = I1 + I2
The current flowing in resistor R3 is given as: -0.143 + 0.429 = 0.286 Amps and the voltage across the resistor R3 is given as : 0.286 x 40 = 11.44 volts
Problem: 10
Find the current in a circuit using Kirchhoff's voltage law