The introduction to the full impulse voltages as defined in the previous section leads to simple circuits for the generation of the necessary wave shapes. The rapid increase and slow decay can obviously be generated by discharging circuits with two energy storages, as the wave shape may well be composed by the superposition of two exponential functions.
Again the load of the generators will be primarily capacitive, as insulation systems are tested. This load will therefore contribute to the stored energy. A second source of energy could be provided by an inductance or additional capacitor. For lightning impulses mainly, a fast discharge of pure inductor is usually impossible, as h.v. chokes with high energy content can never be built without appreciable stray capacitances. Thus a suitable fast discharge circuit will always consist essentially of two capacitors.
Single-stage generator circuits Two basic circuits for single-stage impulse generators are shown in Fig. 3.21.The capacitor C1 is slowly charged from a dace. source until the spark gap Gbreaks down. This spark gap acts as a voltage-limiting and voltage-sensitive switch, whose ignition time (time to voltage breakdown) is very short in comparison to T1. As such single-stage generators may be used for charging voltages from some kV up to about 1 MV, the sphere gaps) will offer proper operating conditions.
An economic limit of the charging voltage V0 is, however, a value of about 200 to 250 kV, as too large diameters of the spheres would otherwise be required to avoid excessive in homogeneous field distributions between the spheres. The resistors R1, R2 and the capacitance C2 form the wave shaping network. R1 will primarily damp the circuit and control the front time T1. R2 will discharge the capacitors and therefore essentially control the wave tail.
The capacitance C2 represents the full load, i.e. the object under test as well as all other capacitive elements which are in parallel to the test object (measuring devices; additional load capacitor to avoid large variations of T1/T2, if the test objects are changed). No inductances are assumed so far, and are neglected in the first fundamental analysis, which is also necessary to understand multistage generators. In general this approximation is permissible, as the inductance of all circuit elements has to be kept as low as possible.
Within the ‘discharge’ capacitance C1. As C1 is always much larger than C2, this figure determines mainly the cost of a generator. For the analysis we may use the Laplace transform circuit sketched .which simulates the boundary condition, that for t 0 C1 is charged to V0 and for t > 0 this capacitor is directly connected to the wave shaping network. For the circuit Fig. 3.21(a) the output voltage is thus given by the expression.
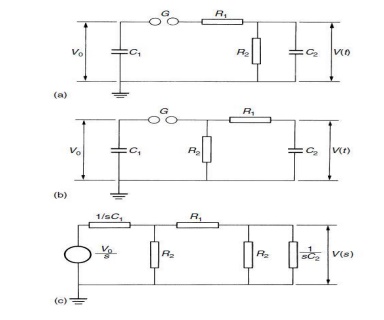
Figure: 3.21Single-stage impulse generator circuits (a) and (b). C1: discharge capacitance. C2 : load capacitance. R1 : front or damping resistance. R2 : discharge resistance. (c) Transform circuit Before starting the analysis, we should mention the most significant parameter of impulse generators. This is the maximum stored energy

For circuit Fig. 3.22 (b) one finds the same general expression eqn , with the following constants; however,
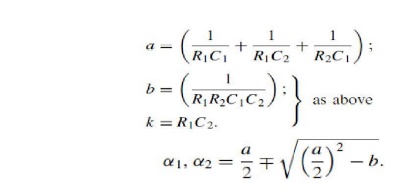
For both circuits, therefore, we obtain from the transform tables the same expression in the time domain:
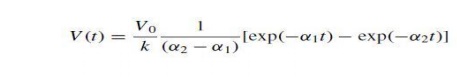
Although one might assume that both circuits are equivalent, a larger difference may occur if the voltage efficiency, 5, is calculated. This efficiency is defined as

Vp being the peak value of the output voltage as indicated . Obviously this value is always smaller than 1 or 100 per cent. It can be calculated by finding tmax from dVt/dt D0; this time for the voltage Vt to rise to its peak value is given by
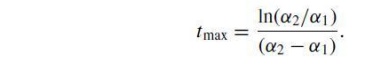
Substituting this equation into eqn one may find
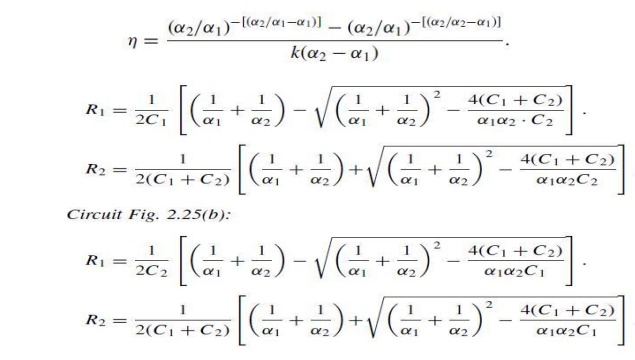
All these equations contain the time constants 1/˛1 and 1/˛2, which depend upon the wave shape. There is, however, no simple relationship between these time constants and the times T1, T2 and Tp as defined in the national or international recommendations, i.e. in Figs 2.23 and 2.24. This relationship can be found by applying the definitions to the analytical expression for Vt,this means to equation. The relationship is irrational and must be computed numerically. The following table shows the result for some selected wave shapes: The standardized nominal values of T1 and T2 are difficult to achieve in practice, as even for fixed values of C1 the load C2 will vary and the exact values for R1 and R2 according to above equation in general not available.
These resistors have to be dimensioned for the rated high voltage of the generator and are accordingly expensive. The permissible tolerances forT1 and T2 are therefore necessary and used to graduate the resistor values. According of the real output voltage V(t) will in addition be necessary if the admissible impulse shape has to be testified. Another reason for such a measurement is related to the value of the test voltage as defined in the recommendations. This magnitude corresponds to the crest value, if the shape of the lightning impulse is smooth.
However, oscillations or an overshoot may occur at the crest of the impulse. If the frequency of such oscillations is not less than 0.5MHz or the duration of overshoot not over 1 sec, a ‘mean curve’ (see Note below) should be drawn through the curve. The maximum amplitude of this ‘mean curve’ defines the value of the test voltage. Such a correction is only tolerated, provided their single peak amplitude is not larger than 5 per cent of the crest value.
Oscillation son the front of the impulse (below 50 per cent of the crest value) are tolerated, provided their single peak amplitude does not exceed 25 percent of the crest value.
It should be emphasized that these tolerances constitute the permitted differences between specified values and those actually recorded by measurements. Due to measuring errors the true values and the recorded ones may be somewhat different. Note. With the increasing application of transient or digital recorders in recording of impulse voltages it became very obvious that the definition of a ‘mean curve’ for the evaluation of lightning impulse parameters of waveforms with oscillations and/or overshoot, as provided by the standards, is insufficient. Any software, written to evaluate the parameters, needs clear instructions which are not yet available. As this matter is still under consideration (by CIGRE Working Group 33.03) and a revision of the current standards may provide solutions, no further comments to this problem are given. The origin of such oscillations or the overshoot can be found in measuring errors as well as by the inductances within every branch of the circuit or the stray capacitances, which will increase with the physical dimensions of the circuit.
As far as inductances are concerned, a general rule for the necessary critical damping of single-stage or – with less accuracy of multistage generators can easily be demonstrated . If individual inductances L1, L2 are considered within the discharge circuit as indicated in Fig. 3.22(a), a second order differential equation determines the output voltage across the load capacitance C2. However, such an equivalent circuit cannot be exact, as additional circuitsrelated to stray capacitances are not taken into account. Thus we may only combine the total inductance within the C1 –C2 circuit to single inductance L, as shown in Fig. 3.22 (b), and neglect the positions of the tail resistors, which have no big influence. This reduces the circuit to a simple damped series resonant circuit, and the critical resistance R D R1 for the circuit to beNon-oscillatory is given by the well-known equation
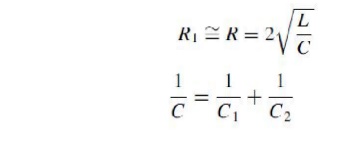
This equation is in general suitable for predicting the limiting values for the front resistor R1. The extremely tedious analytical analysis of circuits containing individual inductances is shown elsewhere. Computer programs for transients may also be used to find the origin of oscillations, although it is difficult to identify good equivalent circuits.
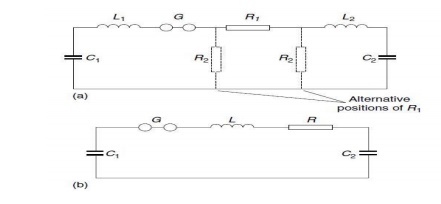
Figure: 3.22 Simplified circuit of impulse generator and load. Circuit showing alternative positions of the wave tail control resistance. (b) Circuit for calculation of wave front oscillations

