Full Subtractor
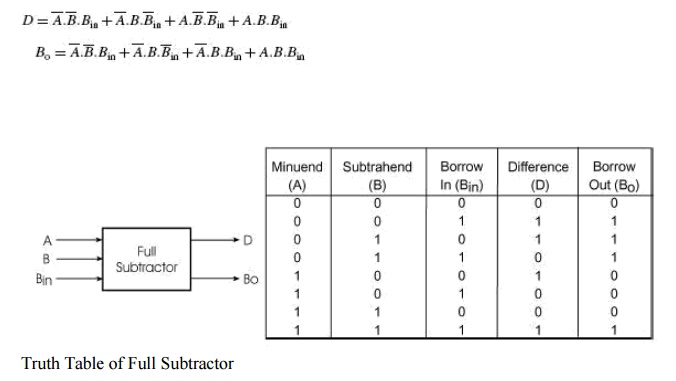
A full subtractor performs subtraction operation on two bits, a minuend and a subtrahend, and also takes into consideration whether a ‘1‘ has already been borrowed by the previous adjacent lower minuend bit or not. As a result, there are three bits to be handled at the input of a full subtractor, namely the two bits to be subtracted and a borrow bit designated as Bin . There are two outputs, namely the DIFFERENCE output D and the BORROW output Bo.
The BORROW output bit tells whether the minuend bit needs to borrow a ‘1‘ from the next possible higher minuend bit. Figure 3.11 shows the truth table of a full subtractor.
The Boolean expressions for the two output variables are given by the equations
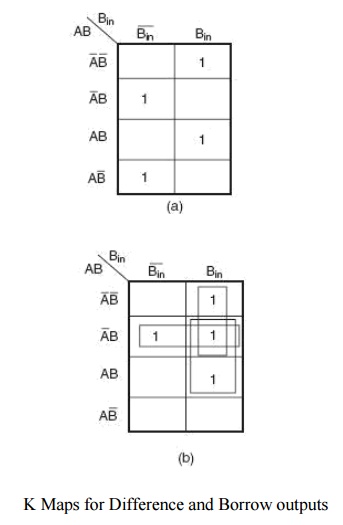
The Karnaugh maps for the two expressions are given in Fig. 3.12(a) for DIFFERENCE output D and in Fig. 3.12(b) for BORROW output Bo. As is clear from the two Karnaugh maps, no simplification is possible for the difference output D. The simplified expression for Bo is given by the equation
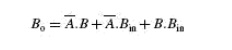
If we compare these expressions with those derived earlier in the case of a full adder, we find that the expression for DIFFERENCE output D is the same as that for the SUM output. Also, the expression for BORROW output Bo is similar to the expression for CARRY-OUT Co. In the case of a half-subtractor, the A input is complemented. By a similar analysis it can be shown that a full subtractor can be implemented with half-subtractors in the same way as a full adder was constructed using half-adders. Relevant logic diagrams are shown in Figs 3.7(a) and (b) corresponding to Figs 3.7(a) and (b) respectively for a full adder. Again, more than one full subtractor can be connected in cascade to perform subtraction on two larger binary numbers. As an illustration, Fig. 3.13 shows a four-bit subtractor.
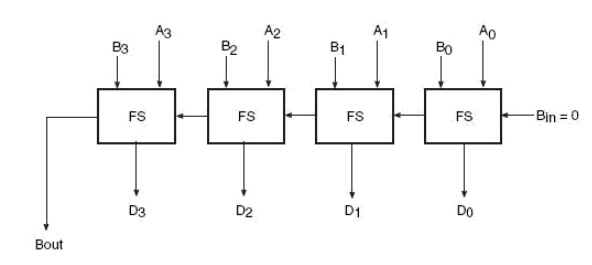
Four Bit Subtractor

