When an insulating material is subjected to an electric field, the material gets heated up due to conduction current and dielectric losses due to polarization. The conductivity of the material increases with increase in temperature and a condition of instability is reached when the heat generated exceeds the heat dissipated by the material and the material breaks down.
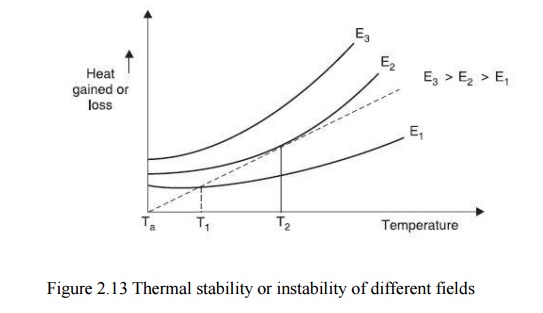
Fig. 2.13 shows various heating curves corresponding to different electric stresses as a function of specimen temperature. Assuming that the temperature difference between the ambient and the specimen temperature is small, Newton’s law of cooling is represented by a straight line.
The test specimen is at thermal equilibrium corresponding to field E1 at temperature T1 as beyond that heat generated is less than heat lost. Unstable equilibrium exists for field E2 at T2,
and for field E3 the state of equilibrium is never reached and hence the specimen breaks down thermally.
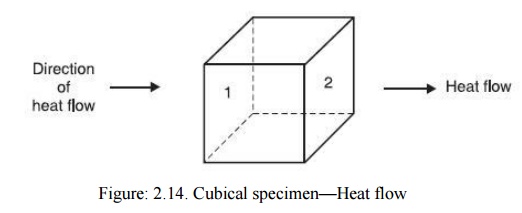
In order to obtain basic equation for studying thermal breakdown, let us consider a small cube (Fig. 2.14) within the dielectric specimen with side Δx and temperature difference across its faces in the direction of heat flow (assume here flow is along x-direction) is ΔT. Therefore, the temperature gradient is

Here the second term indicates the heat input to the differential specimen. Therefore, the heat absorbed by the differential cube volume
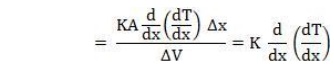
The heat input to the block will be partly dissipated into the surrounding and partly it will raise the temperature of the block. Let CV be the thermal capacity of the dielectric, σ the electrical conductivity, E the electric field intensity. The heat generated by the electric field = σE2 watts, and suppose the rise in temperature of the block is ΔT, in time dt, the power required to raise the temperature of the block by ΔT is
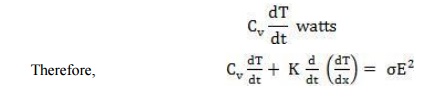
The solution of the above equation will give us the time required to reach the critical
temperature Tc for which thermal instability will reach and the dielectric will lose its insulating properties.
However, unfortunately the equation can be solved in its present from CV, K and σ is all functions of temperature and in fact σ may also depend on the intensity of electrical field.
Therefore, to obtain solution of the equation, we make certain practical assumptions and we consider two extreme situations for its solution
Table: 2.3 Thermal breakdown voltage

Table 2.3 gives for thick specimen, thermal breakdown values for some dielectric under a.c. and d.c. voltages at 20°C.

