CLASSICAL GAS LAWS
In the absence of electric or magnetic fields charged particles in weakly ionized gases participate in molecular collisions. Their motions follow closely the classical kinetic gas theory.
The oldest gas law established experimentally by Boyle and Mariotte states that for a given amount of enclosed gas at a constant temperature the product of pressure (p) and volume (V) is constant or
pV = C = const. 2.1
In the same system, if the pressure is kept constant, then the volumes V and V0 are related to their absolute temperatures T and T0 (in K) by Gay–Lussac’s law:

When temperatures are expressed in degrees Celsius, eqn (2.2) becomes;
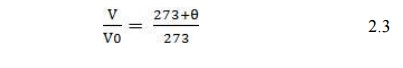
Equation (2.3) suggests that as we approach Ɵ = -273°C the volume of gas shrinks to zero. In reality, all gases liquefy before reaching this value.
According to eqn (2.2) the constant C in eqn (2.1) is related to a given temperature T0 for the volume V0:
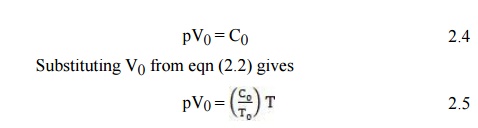
The ratio C0/T0_ is called the universal gas constant and is denoted by R. Equation (2.5) then becomes
pV = RT = C 2.6
Numerically R is equal to 8.314 joules/°Kmol. If we take n as the number of moles, i.e. the mass m of the gas divided by it’s mol-mass, then for the general case eqn (2.1) takes the form
pV = nC = nRT, 2.7
Equation (2.7) then describes the state of an ideal gas, since we assumed that R is a
constant independent of the nature of the gas. Equation (2.7) may be written in terms of gas density N in volume V containing N1 molecules.
Putting N = NA where NA = 6.02 * 1023 molecules/mole, NA is known as the Avogadro’s number. Then eqn (2.7) becomes
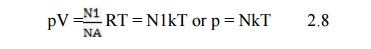
The constant k = R/NA is the universal Boltzmann’s constant (=1.3804 *1023 joules/°K) and N is the number of molecules in the gas.
The fundamental equation for the kinetic theory of gas is derived with the following assumed conditions:
· Gas consists of molecules of the same mass which are assumed spheres.
· Molecules are in continuous random motion.
· Collisions are elastic – simple mechanical.
· Mean distance between molecules is much greater than their diameter

