System Response
First-order system time response
v Transient
v Steady-state
Second-order system time response
v Transient
v Steady-state
First Order System
Y s / R(s) = K / (1+ K+sT) = K / (1+sT)
Step Response of First Order System
Evolution of the transient response is determined by the pole of the transfer function at s=-1/t where t is the time constant
Also, the step response can be found:

Second-order systems
LTI second-order system
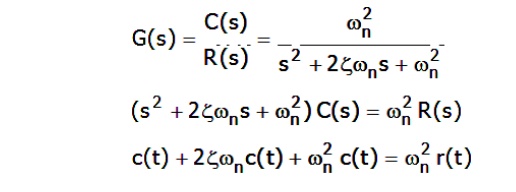


Second order system responses
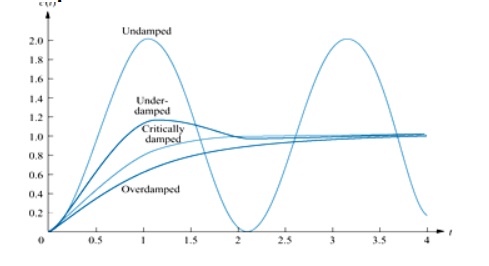
Overdamped response: Poles: Two real at
- σ 1 - - σ 2
Natural response: Two exponentials with time constants equal to the reciprocal of the pole location
C( t)= k1 e-ζ1+ k2 e-ζ2
Poles: Two complex at
Underdamped response:
-σ1±jWd
Natural response: Damped sinusoid with an exponential envelope whose time constant is equal to the reciprocal of the pole‗s radian frequency of the sinusoid, the damped frequency of oscillation, is equal to the imaginary part of the poles
Undamped Response:
Poles: Two imaginary at
±jW1
Natural response: Undamped sinusoid with radian frequency equal to the imaginary part of the poles
C(t) = Acos(w1t-φ)
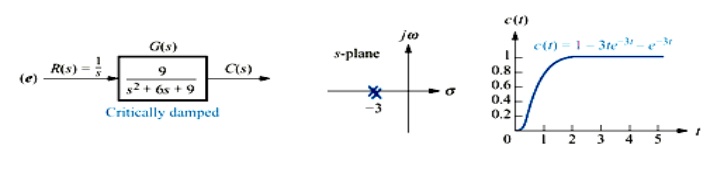
Critically damped responses:
Poles: Two real at
Natural response: One term is an exponential whose time constant is equal to the reciprocal of the pole location. Another term product of time and an exponential with time constant equal to the reciprocal of the pole location.
Second order system responses damping cases
Second- order step response
Complex poles


