State space representation for discrete time systems
The dynamics of a linear time (shift)) invariant discrete-time system may be expressed in terms state (plant) equation and output (observation or measurement) equation as follows
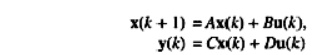
Where x(k) an n dimensional slate rector at time t =kT. an r-dimensional control (input) vector y(k). an m-dimensional output vector ,respectively, are represented as
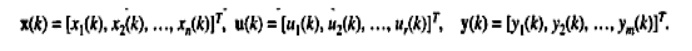
The parameters (elements) of A, an nX n (plant parameter) matrix. B an nX r control (input) matrix, and C An m X r output parameter, D an m X r parametric matrix are constants for the LTI system. Similar to above equation state variable representation of SISO (single output and single output) discrete-rime system (with direct coupling of output with input) can be written as
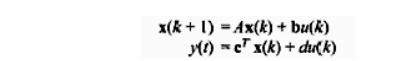
Where the input u, output y and d. are scalars, and b and c are n-dimensional vectors. The concepts of controllability and observability for discrete time system are similar to the continuous-time system. A discrete time system is said to be controllable if there exists a finite integer n and input mu(k); k [0,n 1] that will transfer any state (0) x0 = bx(0) to the state xn at k = n n.

