Routh Hurwitz Criterion
Goal: Determining whether the system is stable or unstable from a characteristic equation in polynomial form without actually solving for the roots Routh‘s stability criterion is useful for determining the ranges of coefficients of polynomials for stability, especially when the coefficients are in symbolic (non numerical) form.
To find K mar & ω
A necessary condition for Routh’s Stability
A necessary condition for stability of the system is that all of the roots of its characteristic equation have negative real parts, which in turn requires that all the coefficients be positive.
A necessary (but not sufficient) condition for stability is that all the coefficients of the polynomial characteristic equation are positive & none of the co-efficient vanishes.
Routh‘s formulation requires the computation of a triangular array that is a function of the coefficients of the polynomial characteristic equation.
A system is stable if and only if all the elements ofthe first column of the Routh array are positive
Method for determining the Routh array
Consider the characteristic equation
a(S) =1X Sn+a1 Sn-1+ a2 Sn-2+……+ an-1 S1+ a0 S0
Routh array method
Then add subsequent rows to complete the Routh array
Compute elements for the 3rd row:
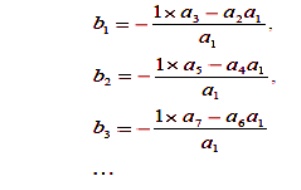
Given the characteristic equation,
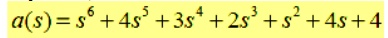
Is the system described by this characteristic equation stable?
Answer:
All the coefficients are positive and nonzero
Therefore, the system satisfies the necessary condition for stability
We should determine whether any of the coefficients of the first column of the Routh array are negative.

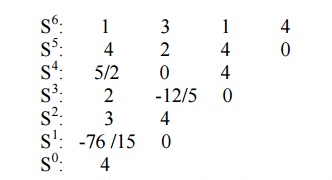
The elements of the 1st column are not all positive. Then the system is unstable
Special cases of Routh’s criteria:
Case 1: All the elements of a row in a RA are zero
Form Auxiliary equation by using the co-efficient of the row which is just above the row of zeros.
Find derivative of the A.E.
Replace the row of zeros by the co-efficient of dA(s)/ds
Complete the array in terms of these coefficients.
analyze for any sign change, if so, unstable
no sign change, find the nature of roots of AE
non-repeated imaginary roots - marginally stable
repeated imaginary roots – unstable
Case 2:
First element of any of the rows of RA is
Zero and the same remaining row contains atleast one non-zero element
Substitute a small positive no. ‗ε‗ in place of zero and complete the array. Examine the sign change by taking Lt ε = 0

