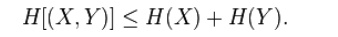ENTROPY:
Entropy is the average amount of information contained in each message received.
Here, message stands for an event, sample or character drawn from a distribution or data stream. Entropy thus characterizes our uncertainty about our source of information. (Entropy is best understood as a measure of uncertainty rather than certainty as entropy is larger for more random sources.) The source is also characterized by the probability distribution of the samples drawn from it.
ü Formula for entropy:
Information strictly in terms of the probabilities of events. Therefore, let us suppose that we have a set of probabilities (a probability distribution) P = {p1, p2, . . . , pn}. We define entropy of the distribution P by
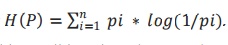
. Shannon defined the entropy of the a discrete random variable X with possible values {x1, ..., xn} and probability mass function P(X) as: Here E is the expected value operator, and I is the information content of X. I(X) is itself a random variable. One may also define the conditional entropy of two events X and Y taking values xi and yj respectively, as
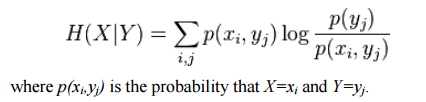
ü Properties:
· If X and Y are two independent experiments, then knowing the value of Y doesn't influence our knowledge of the value of X (since the two don't influence each other by independence):
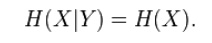
· The entropy of two simultaneous events is no more than the sum of the entropies of each individual event, and are equal if the two events are independent. More specifically, ifX and Y are two random variables on the same probability space, and (X,Y) denotes their Cartesian product, then