A circuit or a group of circuit connected together as a system is said to be stable, if its o/p reaches a fixed value in a finite time. (or) A system is said to be unstable, if its o/p increases with time instead of achieving a fixed value. In fact the o/p of an unstable sys keeps on increasing until the system break down. The unstable system are impractical and need be made stable. The criteriangn for stability is used when the system is to be tested practically. In theoretically, always used to test system for stability , ex: Bode plots.
Bode plots are compared of magnitude Vs Frequency and phase angle Vs frequency. Any system whose stability is to be determined can represented by the block diagram.
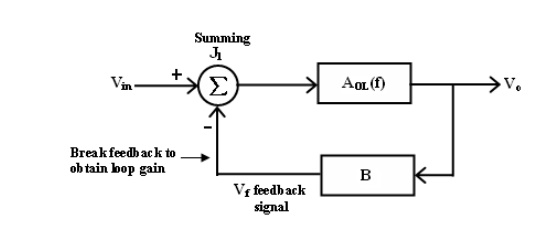
The block between the output and input is referred to as forward block and the block between the output signal and f/b signal is referred to as feedback block. The content of each block is referred
―Transfer frequency‘ From fig we represented it by AOL (f) which is given
by AOL (f) = V0 /Vin if Vf = 0. -----(1)
where AOL (f) = open loop volt gain. The closed loop gain Af is given by
AF = V0 /Vin
AF = AOL / (1+(AOL ) (B) ----(2)
B = gain of feedback circuit.
B is a constant if the feedback circuit uses only resistive components. Once the magnitude Vs frequency and phase angle Vs frequency plots are drawn, system stability may be determined as follows
1. Method:1:
Determine the phase angle when the magnitude of (AOL ) (B) is 0dB (or) 1. If phase angle is > .-1800 , the system is stable. However, the some systems the magnitude may never be 0, in that cases method 2, must be used.
2. Method 2:
Determine the phase angle when the magnitude of (AOL ) (B) is 0dB (or) 1. If phase angle is > .-1800 , If the magnitude is –ve decibels then the system is stable. However, the some systems the phase angle of a system may reach -1800 , under such conditions method 1 must be used to determine the system stability.

