A series RC circuit with initial current I0 in the inductor is connected to a dc voltage V at t = 0. Derive the expression for instantaneous current through the inductor for t>0.
Or
Explain in brief about the step response of series RC circuits.
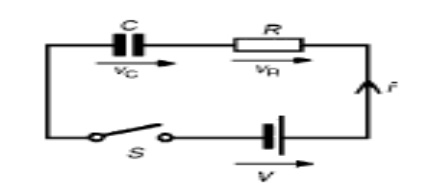
Consider series RC circuit as shown in fig. The switch k is in open state initially. There is no charge on condenser and A0 voltage across it. At instant t = 0, switch k is closed.
Immediately after closing a switch, the capacitor acts as a short circuit, so current at the time of switching is high. A voltage across capacitor is zero at t = 0+. As capacitor acts as a short circuit, the current is maximum and is given by
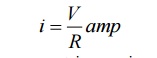
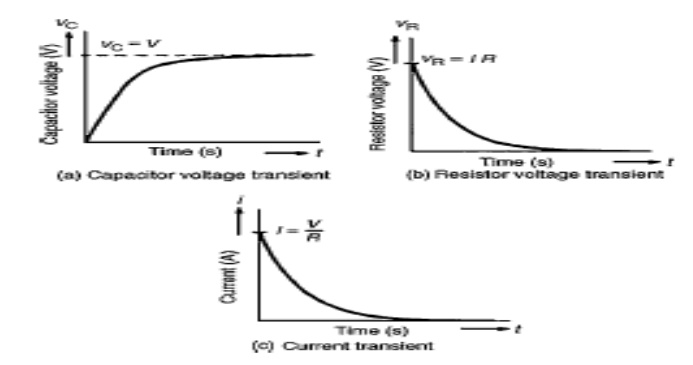
The current is maximum at t=0 + which is charging current. As the capacitor starts charging, the voltage across capacitor VC starts increasing and charging current starts decreasing. After some time, when the capacitor charges to V volts, it achieves steady state. In steady state, it acts as a open circuit so current will be zero finally.
After switching instant applying Kirchoff’s voltage law.
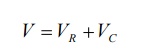
Where VR is voltage across resistor and VC is voltage across capacitor.


When the steady state is achieved, total charge on the capacitor is Q coulombs.
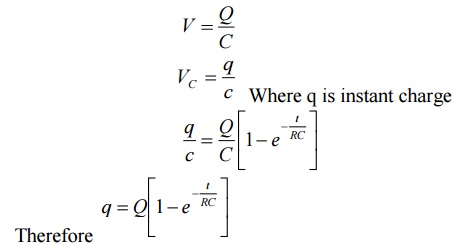
Thus the charge on the capacitor also behaves similar to voltage across capacitor.
Now current can be expressed as

So at t = 0, i = V/R is maximum current and in steady state it becomes zero.
The variation of voltage across capacitor and charging with respect to time is shown in fig.
The term RC in equation of VC is called time constant and denoted by measured in seconds When
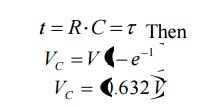
So time constant of series RC circuit is defined as time required by capacitor voltage to rise from zero to 0.632 of its final steady state value during charging.
Thus, time constant of RC circuit can be defined as time in seconds, during which the voltage across capacitor would reach its final steady state value of its rate of change was maintained constant at its initial value throughout charging period.

