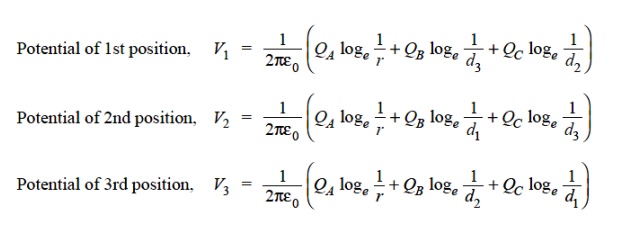Capacitance of a Single Phase Two-Wire Line
Consider a single phase overhead transmission line consisting of two parallel conductors A and B spaced d metres apart in air. Suppose that radius of each conductor is r metres. Let their respective charge be + Q and − Q coulombs per metre length. The total p.d. between conductor A and neutral “infinite” plane is
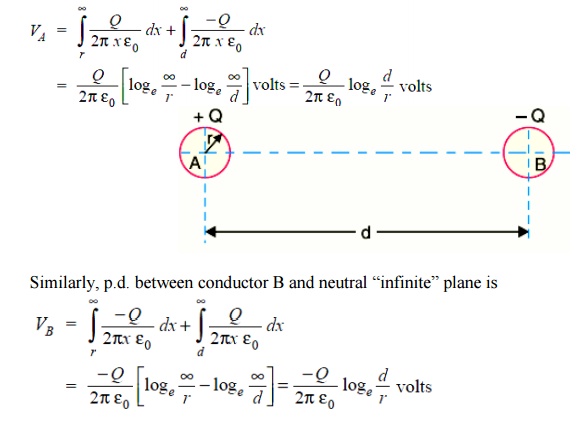
Both these potentials are w.r.t. the same neutral plane. Since the unlike charges attract each other, the potential difference between the conductors is
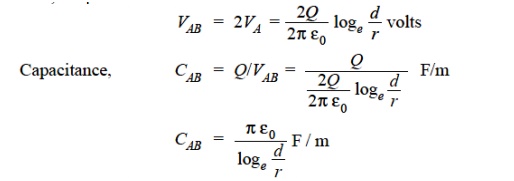
Capacitance to neutral
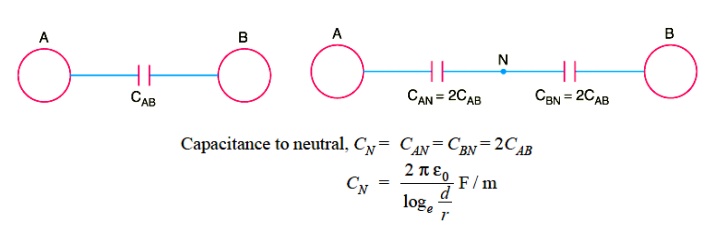
Equation ( i) gives the capacitance between the conductors of a two-wire line Often it is desired to know the capacitance between one of the conductors and a neutral point between them. Since potential of the mid-point between the conductors is zero, the potential difference between each conductor and the ground or neutral is half the potential difference between the conductors. Thus the capacitance to ground or capacitance to neutral for the two-wire line is twice the line-to-line capacitance
The reader may compare eq. ( ii) to the one for inductance. One difference between the equations for capacitance and inductance should be noted carefully. The radius in the equation for capacitance is the actual outside radius of the conductor and not the GMR of the conductor as in the inductance formula. Note that eq. ( ii) applies only to a solid round conductor.
1. CAPACITANCE OF A 3-PHASE OVERHEAD LINE
In a 3-phase transmission line, the capacitance of each conductor is considered instead of capacitance from conductor to conductor. Here, again two cases arise viz., symmetrical spacing and unsymmetrical spacing.
( i) Symmetrical Spacing
Fig shows the three conductors A, B and C of the 3-phase overhead transmission line having charges QA , QB and QC per meter length respectively. Let the conductors be equidistant (d meters) from each other. We shall find the capacitance from line conductor to neutral in this symmetrically spaced line. Referring to Fig,
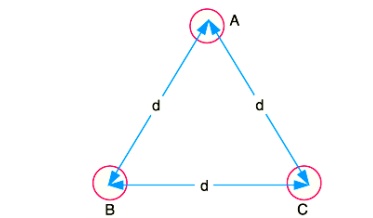
Overall potential difference between conductor A and infinite neutral plane is given by
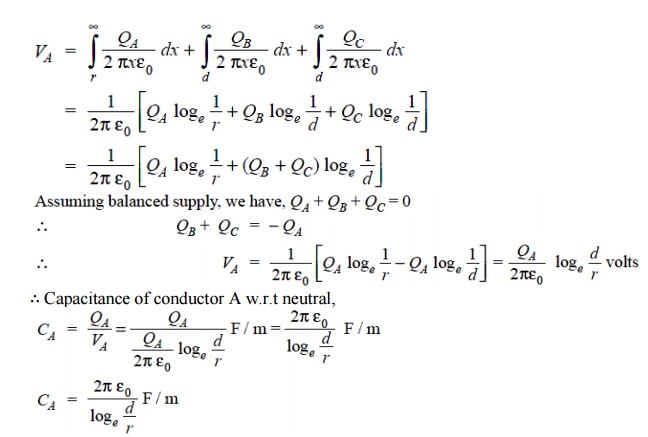
Note that this equation is identical to capacitance to neutral for two-wire line. Derived in a similar manner, the expressions for capacitance are the same for conductors B and C.
(ii) Unsymmetrical spacing.
Fig. shows a 3-phase transposed line having unsymmetrical spacing. Let us assume balanced conditions i.e. QA + QB + QC = 0.
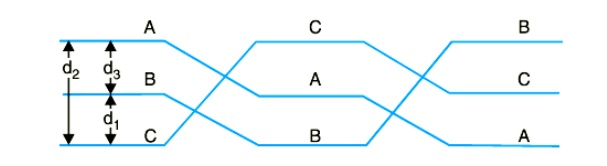
Considering all the three sections of the transposed line for phase A,